
A photo of the Nintendo 64's motherboard with the main chips labeled. Motherboard photo courtesy of Evan-Amos

A photo of the Nintendo 64's motherboard with the main chips labeled. Motherboard photo courtesy of Evan-Amos
The Nintendo 64 features two processors:
The RCP is split into two different sections (not including the I/O chip):
The CPU and the RCP work in parallel to process and render the game. The focus of these pages will be on the RDP, which is the part that handles the actual drawing of polygons. But in order to render textures, the RCP needs access to the data from somewhere.
The obvious solution would be to fetch the data from RAM, but this brings a few problems. First of all, the CPU also has access to the data in RAM, so there is no guarantee that the textures will not be modified as the RDP is trying to render polygons. The other problem is the fact that RAM can be slow to access. Because of this, processors have a little memory chip embedded into them called a cache. Caches are usually very small in size (usually just a few kilobytes), but are incredibly fast to read and write. The RDP contains a single cache called TMEM, which will be covered in more depth in the TMEM page.
Computers work on electricity, and for simplicity sake, lets say that electricity only exists in two different states: On and Off (1 and 0). Because computers only work with 0's and 1's, there needs to be a way to convert numbers into a format that computers can understand.
When you count, you probably do it in "base ten". This means that you only use a combination of ten different symbols to identify your numbers. These are:
0 1 2 3 4 5 6 7 8 9
When you start counting numbers, you start from 0 and go all the way to 9. But when you try to count past 9, the next number is 10, which is composed of two symbols instead of just one. Because there is no symbol for a number past 9, you simply reset 9 back to 0, and you increase the number next to the 9 (which went from 0 to 1).
Binary numbers work in the exact same way, except instead of having ten different symbols, you only have two: 0 and 1. This is called "base two". An individual 0 or 1 is called a bit.
Counting in binary follows the exact same pattern as counting in base ten. Here is an example table counting to 10 (Note, I have included extra 0's on the left side of each number to make the table easier to read):
| Base 10 || | Base 2 |
|---|---|
| 00 | 0000 |
| 01 | 0001 |
| 02 | 0010 |
| 03 | 0011 |
| 04 | 0100 |
| 05 | 0101 |
| 06 | 0110 |
| 07 | 0111 |
| 08 | 1000 |
| 09 | 1001 |
| 10 | 1010 |
Another way to visualize binary numbers is that each digit represents a power of two. For instance, the number 342, in base 10, can be broken down like this:
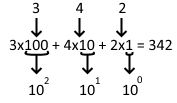
342 in base 2 is 101010110. You can break it down like this:
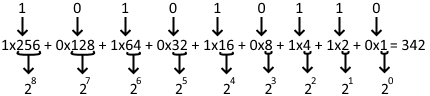
Now of course, this explanation is missing a lot of key information, such as how negative numbers are represented, and how to write decimals. These are not important to understand what is going to be discussed in this help document, therefore if you wish to learn more about binary notation, you'll need to research that on your own.
In computer science, it is convention to group binary numbers in groups of 8. That's why processors tend to be 8, 16, 32, or 64 bit, and not some other number. A group of 8 bits is referred to as a byte. This means that a byte can range from 0 to 255 (which is equivalent to eight 1's).
You would think that in computer science, the preferred way of counting numbers is with base eight (also known as octal), but that is not the case. Instead, base sixteen is used, which is known as hexadecimal (or hex for short). So your first question might be: "If we only have ten different symbols to represent numbers, how do you represent numbers like 10 and 11?". The answer is that the letters A through F are used instead. This means that 10 is represented by A, 11 by B, etc... All the way until 15, which is F.
There are quite a few ways to begin a hexadecimal number's representation, but the most common is to start with 0x. Some programming languages perfer to use a $ symbol to indicate the start of a hexadecimal number, but the former is much more common.
Base sixteen is useful to us because it makes it very obvious when a a byte starts or begins. The largest number possible with a single byte is 255, which is represented as 0xFF in hexadecimal. Knowing that, you should understand that you can identify bytes by simply counting two letters or numbers. As an example, the number 342 in hexadecimal notation is represented as 0x0156. Looking at it, you should be able to conclude that you need two bytes to be able to store the number 342 in memory.
From here on out, there is going to be a lot of hexadecimal numbers, so it is important that you understand them well.
It was mentioned that the CPU generates a list of commands which get sent to the RCP. These instructions are received by the RSP and then sent to the RDP for rendering. There is a very long list of the different types of display list commands available in the N64 reference manual which will not be covered in these pages.
Display lists come in two different formats, dynamic and static. In this manual, display lists will be written in static format. It is, however, very easy to swap between the two, so it should not be too much of a problem if you wish to use dynamic display lists instead.
Your programmer, in order to generate a display list to load your texture, needs to know what type of format you exported your images as, as well as their size (in pixels). So it is important that you tell him about that!